相关分析是用于研究多个变量之间相互关系的统计方法,最早由英国统计学家卡尔·皮尔逊(Karl Pearson)于1896年提出。皮尔逊通过对变量间线性关系的深入研究,提出了“皮尔逊相关系数”(Pearson Correlation Coefficient),标志着相关分析方法的诞生。随着统计学的发展,相关分析逐渐扩展,形成了适用于不同数据类型和研究场景的多种相关系数。皮尔逊相关系数用于衡量两个变量之间的线性关系,尤其适合连续数据的分析。而在面对非线性关系或等级数据时,研究者提出了其他相关分析方法,如斯皮尔曼等级相关系数和肯德尔等级相关系数。这些方法为处理不同类型的数据提供了更加灵活的手段。从皮尔逊的贡献开始,相关分析作为统计学中不可或缺的工具,经历了持续的发展和完善。无论是线性相关的皮尔逊相关系数,还是用于处理非线性和等级数据的斯皮尔曼和肯德尔相关系数,它们都在科学研究、经济分析、心理学等多个领域中发挥着重要作用。通过相关分析,研究者能够更清晰地理解变量之间的关系,并为后续的模型构建和统计推断提供坚实的理论基础。
相关系数计算步骤 散点图矩阵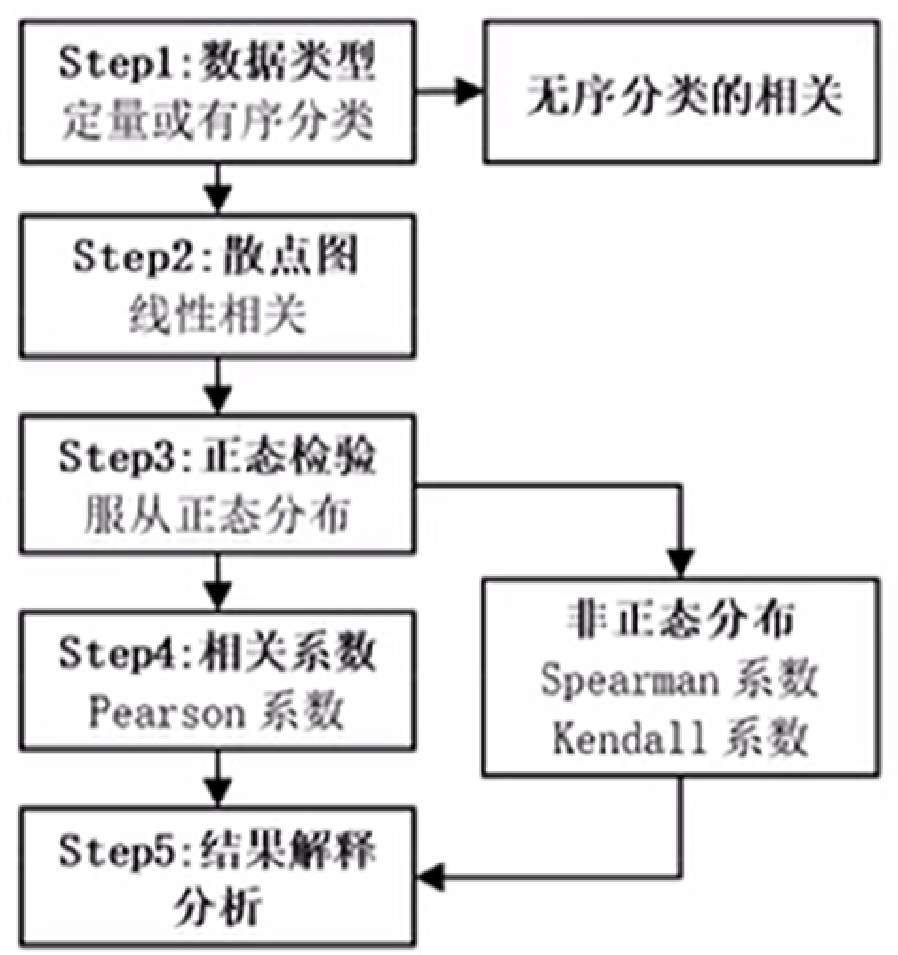
相关分析是用于研究变量之间相互关系的重要统计工具。为了更直观、便捷地理解变量之间的相关性,统计学中常用相关表和相关图两种形式进行呈现和分析。它们不仅能够帮助研究者识别变量之间的关系强度,还能为后续的数据分析和模型构建提供重要的参考依据。
1.1 相关表 (Correlation Matrix)相关表,又称为相关系数矩阵,是展示多个变量之间两两相关性的一种表格形式。每个变量之间的相关性用一个相关系数来表示,通常以数值形式展示在矩阵的相应位置中。相关表的行和列都列出所研究的变量名,而表中的值是相应变量的皮尔逊相关系数、斯皮尔曼等级相关系数或肯德尔相关系数。
例如,如果我们分析三个变量\(X_1\)、\(X_2\)和\(X_3\),它们之间的相关系数矩阵可以表示为:
\[\left[ \begin{matrix} r(X_1, X_1) & r(X_1, X_2) & r(X_1, X_3) \\ r(X_2, X_1) & r(X_2, X_2) & r(X_2, X_3) \\ r(X_3, X_1) & r(X_3, X_2) & r(X_3, X_3) \\ \end{matrix} \right]\]
其中,\(r(X_1, X_2)\) 表示变量\(X_1\) 与\(X_2\)之间的相关系数。如果两个变量的相关系数接近1,表示它们之间存在强正相关;接近-1,则表示强负相关;接近0,说明变量之间几乎没有线性关系。对角线上的值总是1,因为任何变量与自身的相关系数总是完全正相关。
应用场景金融市场分析:在金融领域中,相关表常用于分析股票、债券等资产之间的关系,以帮助投资者进行风险分散或资产组合优化。
心理学研究:研究者可以通过相关表分析不同心理测试项之间的相关性,识别出哪些心理变量是相关的或相互影响的。
经济学分析:在经济研究中,经济指标(如GDP、通货膨胀率、失业率等)的相关系数能够帮助预测和解释宏观经济现象。
1.2 相关图 (Correlation Plot)相关图是相关分析的可视化形式,能够更直观地展示变量间的相关关系。相比于相关表中数值的表达,相关图通过颜色、大小或其他图形元素更为生动地传达信息。常见的相关图有散点图、热力图等形式。
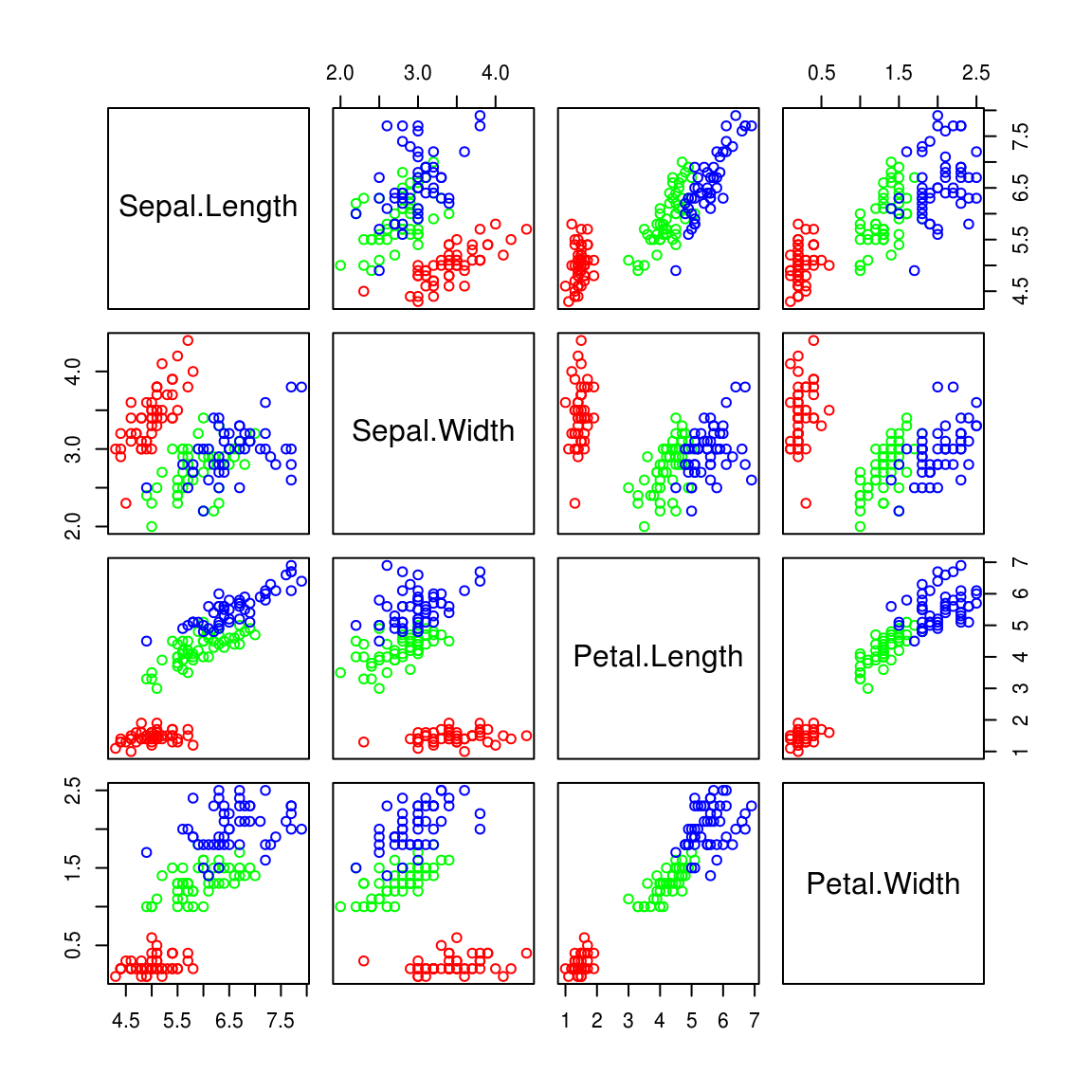
散点图矩阵 (Scatter Plot Matrix)散点图矩阵是通过将每对变量的散点图展示在矩阵中的形式来可视化多个变量之间的关系。矩阵的每一行和每一列都表示一个变量,矩阵中的每一个散点图展示了两个变量的联合分布情况。
例如,两个高度正相关的变量\(X\)和\(Y\)在散点图中呈现出接近于一条直线的形状。散点图不仅可以展示相关性,还能够揭示变量间的非线性关系或异常值的存在。散点图矩阵常用于探索数据集的结构,特别是在多元回归分析前,可以帮助研究者快速识别出变量间潜在的线性或非线性关系。
相关热力图 (Correlation Heatmap)热力图是另一种常见的相关图形式,它通过颜色的深浅来表示不同变量间相关性的强弱。在热力图中,每个颜色块对应相关系数矩阵中的一个相关系数值。颜色越深,表示变量间的相关性越强,颜色越浅,则表示相关性越弱。一般情况下,颜色会从正相关到负相关呈现为从深蓝到深红的渐变。热力图在复杂数据分析中尤为常见,尤其是在大规模数据集中,研究者可以通过直观的色彩变化快速识别变量之间的相关关系。例如,在基因组学研究中,相关热力图常用于分析多个基因表达量之间的相关性;在金融领域,热力图帮助投资者直观地理解不同资产之间的相关性,从而优化投资组合。
对角相关图 (Correlogram)对角相关图是一种结合了散点图和热力图的信息展示形式。它将相关系数通过不同的颜色、符号或者大小标记在变量间的交点位置,同时在对角线上展示变量的单变量分布。这种图形形式通过单个图形可以包含非常丰富的信息,便于研究者观察变量间的相关性和分布特征。对角相关图在金融、心理学、社会科学等多种学科中广泛应用,尤其是在多元数据分析中,能够提供更多维度的信息。
二、三种相关系数的计算公式与应用常用的相关系数的度量有三种,随着时间的推移,研究者们意识到皮尔逊相关系数的局限性,开始发展其他适应性更强的相关系数。为了应对非线性关系和等级数据,斯皮尔曼等级相关系数(Spearman Rank Correlation Coefficient)和肯德尔等级相关系数(Kendall Rank Correlation Coefficient)相继被提出。
2.1 皮尔逊相关系数 (Pearson Correlation Coefficient)皮尔逊相关系数是用于衡量两个连续变量之间线性相关程度的统计量,其计算公式为:
\[r_{xy} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}} \]
其中,\(x_i\)和\(y_i\)分别是两个变量的观测值,\(\bar{x}\)和\(\bar{y}\)是各自的均值,\(n\)是样本大小。皮尔逊相关系数衡量的是变量之间的线性关系,它假设数据是服从正态分布的。
应用场景股票市场的收益率分析:在金融市场中,皮尔逊相关系数常被用来衡量两个股票之间的收益率关系。
身高与体重的相关性:在生活中,身高和体重通常有一定的正相关关系。
优缺点优点:皮尔逊相关系数易于理解,能准确反映变量之间的线性关系。
缺点:当数据不服从正态分布或存在极端值时,皮尔逊相关系数可能会失真。
2.2 斯皮尔曼等级相关系数 (Spearman Rank Correlation Coefficient)斯皮尔曼等级相关系数是一种基于排名的非参数相关系数,适用于非正态分布数据或非线性关系。其公式为:
\[\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \]
其中,\(d_i\)是两个变量在第\(i\)个样本中的排名差,\(n\)是样本量。
应用场景学生成绩排名:分析两个学科成绩排名的相关性。
满意度调查:在社会学研究中,调查中所涉及的满意度可能并不具备线性关系。
优缺点优点:斯皮尔曼等级相关系数不要求数据服从特定分布,适用于非线性关系的测量。
缺点:斯皮尔曼相关系数只能反映单调关系,不能区分变量间的具体形式。
2.3 肯德尔等级相关系数 (Kendall Rank Correlation Coefficient)肯德尔等级相关系数也是一种非参数相关系数,计算两个变量之间的等级一致性。其公式为:
\[\tau = \frac{\sum C - \sum D}{2} \]
其中,\(C\)是一致对的数量,\(D\)是不一致对的数量,\(n\)是样本大小。
应用场景心理学研究:衡量不同观察者对于同一现象的评估结果是否一致。
企业面试打分:多个面试官对候选人进行打分时,可以用肯德尔相关系数来衡量他们的打分一致性。
优缺点优点:肯德尔相关系数能够更稳定地反映样本中的等级一致性,特别适用于样本量较小的情况。
缺点:与斯皮尔曼相关系数相比,计算复杂度较高,尤其在大规模数据中。
三、相关系数的意义以皮尔逊相关系数示范相关系数度量的内涵。皮尔逊相关系数由英国统计学家卡尔·皮尔逊(Karl Pearson)于1896年提出,是用于衡量两个连续变量之间线性关系强度的统计量。皮尔逊的工作基于当时对生物统计学、遗传学和社会科学等领域的需求,他希望能够通过一种标准化的方式定量表示两个变量的相关程度。这种系数为研究者提供了一个便捷工具,用以判断两个变量之间的关联性。相关系数的值介于-1和1之间,数值的大小表示变量间线性关系的强度,而符号表示正相关还是负相关。正相关意味着一个变量的增加伴随着另一个变量的增加,而负相关则意味着一个变量的增加伴随着另一个变量的减少。
3.1 皮尔逊相关系数皮尔逊相关系数(Pearson Correlation Coefficient)定义为两个变量协方差与标准差的比值:
\[r_{xy} = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} \]
其中:
Cov(X,Y) 表示变量 \(X\) 和 \(Y\) 的协方差,
\(\sigma_X\) 和 \(\sigma_Y\) 分别为 \(X\) 和 \(Y\) 的标准差。
协方差度量了两个变量之间的联合变化趋势,标准差则用于标准化协方差,保证相关系数在 \([-1, 1]\) 范围内。
3.2 皮尔逊相关系数的取值我们要证明的是皮尔逊相关系数的绝对值总是小于等于1,即 \(|r_{xy}| \leq 1\)。
协方差的定义:协方差 \(\text{Cov}(X, Y)\) 定义为:
\[\text{Cov}(X, Y) = \mathbb{E}[(X - \mu_X)(Y - \mu_Y)] \]
其中 \(\mathbb{E}\) 表示期望,\(\mu_X\) 和 \(\mu_Y\) 分别为 \(X\) 和 \(Y\) 的均值。
应用柯西-施瓦茨不等式:柯西-施瓦茨不等式指出,对于任意两个随机变量 \(X\) 和 \(Y\),我们有:
\[\mathbb{E}[(X - \mu_X)(Y - \mu_Y)]^2 \leq \mathbb{E}[(X - \mu_X)^2] \cdot \mathbb{E}[(Y - \mu_Y)^2] \]
即:
\[\text{Cov}(X, Y)^2 \leq \sigma_X^2 \sigma_Y^2 \]
标准化协方差:由此得出:
\[\left( \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} \right)^2 \leq 1 \]
这就意味着:
\[|r_{xy}| \leq 1 \]
特例当两个变量存在完全线性关系时相关系数等于1。现在证明当两个变量 \(X\) 和 \(Y\) 存在完全线性关系时,皮尔逊相关系数的绝对值等于1。假设两个变量之间存在如下线性关系:
\[Y = aX + b \]
其中 \(a\) 和 \(b\) 是常数。由于 \(Y\) 是 \(X\) 的线性函数,我们期望相关系数 \(r_{xy}\) 的值为1或-1,具体取决于 \(a\) 的符号。
计算均值:
\(Y = aX + b\),因此: \(\mu_Y = a\mu_X + b\)
计算协方差:
协方差的定义为:
\[\text{Cov}(X, Y) = \mathbb{E}[(X - \mu_X)(Y - \mu_Y)] = \mathbb{E}[(X - \mu_X)(aX + b - a\mu_X - b)] \]
展开得: \(\text{Cov}(X, Y) = a\mathbb{E}[(X - \mu_X)^2] = a\sigma_X^2\)
计算标准差:
\(Y\) 的标准差为:
\[\sigma_Y = \sqrt{\mathbb{E}[(Y - \mu_Y)^2]} = \sqrt{a^2\mathbb{E}[(X - \mu_X)^2]} = |a|\sigma_X \]
计算相关系数:
相关系数 \(r_{xy}\) 为:
\[r_{xy} = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} = \frac{a\sigma_X^2}{\sigma_X |a|\sigma_X} = \frac{a}{|a|} \]
因此,\(r_{xy} = 1\) 当 \(a > 0\),而 \(r_{xy} = -1\) 当 \(a < 0\)。
这就证明了当两个变量之间存在完全线性关系时,皮尔逊相关系数的绝对值等于1。皮尔逊相关系数通过衡量两个变量之间的线性关系强度,为我们提供了定量化的工具,用以研究变量间的相互作用。我们证明了其值始终介于-1到1之间,且当两个变量存在完全线性关系时,相关系数的绝对值等于1。这一系数在统计学、经济学、心理学等多个领域具有广泛应用,为相关分析提供了坚实的数学基础。
四、案例分析有若干个样品,每个样品有n个特征,则相关系数可以表示两个样品间的相似程度。借此可以对样品的亲疏远近进行距离聚类。例如9个小麦品种(分别用A1,A2,...,A9表示)的6个性状资料见下表,作相关系数计算并检验。
品种编号 X1(冬季分蘖) X2(株高) X3(每穗粒数) X4(千粒数) X5(抽穗期) X6(成熟期)相关分析是统计学中用于研究变量间相互关系的重要工具,通过衡量变量之间的相关性来探讨它们是否具有某种联系。常用的三种相关系数包括皮尔逊相关系数、斯皮尔曼等级相关系数和肯德尔等级相关系数,它们各自适用于不同的数据类型和应用场景。皮尔逊相关系数主要用于测量两个连续变量之间的线性关系;斯皮尔曼等级相关系数则适用于非正态分布或非线性关系的数据,通过变量的排名来评估其单调相关性;肯德尔等级相关系数则更加注重变量间等级排序的相对一致性,常用于研究者或评审者打分一致性分析。