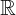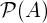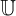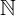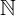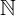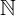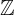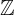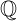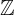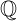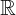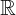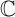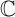集合论的集合符号（Ø，U，{}，∈，...）

集合理论和概率的集合符号列表。

集合理论符号表 符号 符号名称 含义/
定义 例
{}   设置   元素集合   A = {3,7,9,14}，
B = {9,14,28}  
|   这样   以便   A = { x | X ∈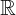

，X <0}  
⋂   路口   属于集合A和集合B的对象   A⋂B = {9,14}  
⋃   联盟   属于集合A或集合B的对象   A⋃B = {3,7,9,14,28}  
⊆   子集   A是B的子集。集合A包含在集合B中。   {9,14,28}⊆{9,14,28}  
⊂   适当子集/严格子集   A是B的子集，但A不等于B。   {9,14}⊂{9,14,28}  
⊄   不是子集   集A不是集B的子集   {9,66}⊄{9,14,28}  
⊇   超集   A是B的超集。集合A包括集合B   {9,14,28}⊇{9,14,28}  
⊃   适当的超集/严格的超集   A是B的超集，但B不等于A。   {9,14,28}⊃{9,14}  
⊅   不超集   集A不是集B的超集   {9,14,28}⊅{9,66}  
2一   功率设定   A的所有子集      

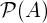
  功率设定   A的所有子集      
A = B   平等   两组都有相同的成员   A = {3,9,14}，
B = {3,9,14}，
A = B  
一ç   补充   所有不属于集合A的对象      
一种'   补充   所有不属于集合A的对象      
A \ B   相对互补   属于A而不属于B的对象   A = {3,9,14}，
B = {1,2,3}，
A \ B = {9,14}  
AB   相对互补   属于A而不属于B的对象   A = {3,9,14}，
B = {1,2,3}，
A-B = {9,14}  
A∆B   对称差异   属于A或B但不属于它们的交集的对象   A = {3,9,14}，
B = {1,2,3}，
A ∆ B = {1,2,9,14}  
⊖   对称差异   属于A或B但不属于它们的交集的对象   A = {3,9,14}，
B = {1,2,3}，
A = B = {1,2,9,14}  
一∈A   的元素，
属于   设定会员   A = {3,9,14}，3∈A  
X ∉A   不是元素   没有固定的会员资格   A = {3,9,14}，1∉A  
（a，b）   有序对   2个元素的集合      
A×B   笛卡尔积   A和B中所有有序对的集合      
| A |   基数   集A的元素数   A = {3,9,14}，| A | = 3  
＃一种   基数   集A的元素数   A = {3,9,14}，＃A = 3  
|   竖线   这样   A = {x | 3 <x <14}  
ℵ 0   空   自然数的无限基数      
ℵ 1   炔属   可数序数集的基数      
Ø   空集   Ø= {}   A =Ø  

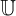
  通用集   所有可能值的集合      
ℕ 0   自然数/整数集（零）  

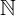
0 = {0,1,2,3,4，...}   0∈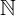

0  
ℕ 1   自然数/整数集（不包含零）  

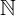
1 = {1,2,3,4,5，...}   6∈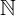

1  
ℤ   整数集  

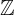
= {...- 3，-2，-1,0,1,2,3，...}   -6∈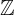

 
ℚ   有理数集  

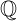
= { x | X =一个/ b，一个，b ∈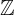

和b ≠0}   2/6∈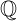

 
ℝ   实数集  

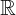
= { x | -∞< x <∞}   6.343434∈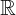

 
ℂ   复数集  

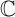
= { z | z = a + bi，-∞< a <∞，-∞< b <∞}   6 + 2我∈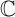

 

统计符号►